ドラクエの世界が見たい

「ドラクエの世界は地球のような球ではなく，ドーナツ型をしている．」という話は豆知識としてしばしば聞く話である．聞いたことがない方はこのような説明を見ると納得できるだろう．だがしかしドーナツ型というのも実はおかしな話である．地図が正確すぎるのだ．（偶然にもつい最近某掲示板でスレッドが立っていたようだ．）

我々が住んでいる地球は球体（正確には回転楕円体）であり，全世界をひずみなく平面に移すこと，つまり完璧な世界地図を作ることは不可能である．微分幾何の分野では正確な地図を書くことができる曲面のことを可展面というが，可展面であるための必要十分条件はガウス曲率が恒等的に0であることが知られている．ガウス曲率が恒等的に0な面は円柱の側面，円錐の面，そして曲線の接線で構成される面（接線曲面）の3パターンとその貼り合わせであり，半径の球面のガウス曲率はであるため完全な地図は作れないのである．

そしてこれはドーナツも例外ではなく，そのガウス曲率は非零であるため完全な地図は作れない．よってドーナツ世界の地図上の場所によって実際の距離は変化しているはずであるが，ドラクエはそうなっていない．どこでも1マスの大きさは一定のドット数で表されている．

では，ドラクエの世界は曲面として全くありえないのかというとそうでもない．ここまであえて「トーラス」という言葉を使わず「ドーナツ」と言ってきたが，ドラクエの世界は平坦トーラスというトーラスの一種と考えることができるのである．だが，この平坦トーラスというやつは厄介なやつでなんと4次元空間の曲面である．4次元空間を考えるのはとても難しいが，なんとか平坦トーラスがどんな形か考えてみよう．

（以下，難しければ最後だけ読めばよい）

4次元空間は3次元空間+時間と考えることができる．つまり4次元空間の物体は時間的に形が変化する3次元物体ととらえることができる．よってある時刻で4次元物体を見れば3次元のものとして我々にも想像できる．これはつまりある時間で断面を作ることになるが，断面を作るとその物体の次元は1つ小さくなる．よって4次元空間の曲面である平坦トーラスをある時刻で見ると曲線になっているはずである．

このことは平坦トーラスを考えるうえで大きなヒントになる．それでは，この世界地図がどのように閉曲面をなしているのかを説明しよう．

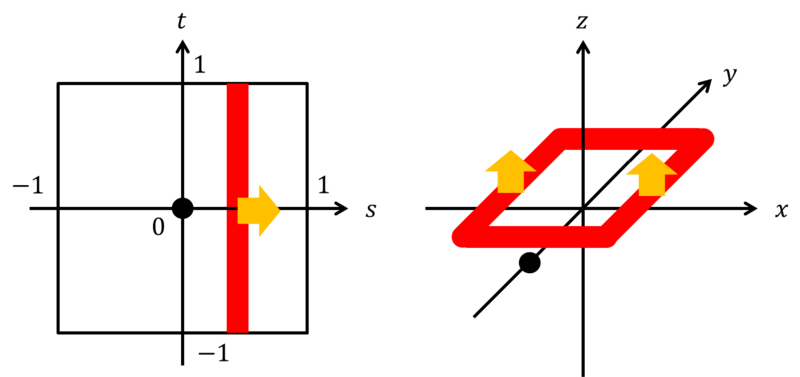
この地図上で閉曲線を書くとそれは当然4次元曲面上で閉曲線をなしているはずである．例えば下図の赤線のような線を考える．上と下はつながっているためこの線は閉曲線である．

地図上にによる座標をつけ，今考えている空間をの3次元空間+の時間からなるものとしよう．そしてとりあえずこの赤線に対応する閉曲線はある時刻の平面内の閉曲線であるとし，原点はに写っているとする．

この赤線は平面上で動いても平坦トーラス上では閉曲線を保つ．今は赤線は上にいるが，これをと移動させると元の位置に連続的に戻るはずである．さらに地図と平坦トーラスの場所は1対1に対応しているため赤線は4次元空間の座標として同じところを通らない．要するに輪っかが動いて元に戻ればよい．4次元空間の一筆書きのようなものである．

初期時刻をとし，とりあえず時刻とともにの高さまで赤線を軸正の方向に動かす．ここで時刻はになったとしよう．

元の位置に戻さないといけないので，今度は軸負の方向に移動させる．さっき通ったところであるが，時刻が異なるので4次元空間的には違う場所である．までおろした時点で時刻はになったとする．

的には輪っかはもとに戻ったが，時刻が異なるので4次元空間的には違う場所である．なのでこれでゴールではない．元に戻るためには時間を戻さなくてはならない．しかし単に今までの運動を逆回しにするのでは4次元空間的に同じ場所を辿ることになるのでNGである．そこで，時間を遡りながら軸負の方向に輪っかを動かす．までおろしたところで時刻はまで戻っているとする．さっき時刻での高さに動かしていた赤線が見える．

このまま時間を遡りながらでの位置まで赤線をあげる．さっきのやつと徐々に距離が縮まり，最後に合流して終了である．

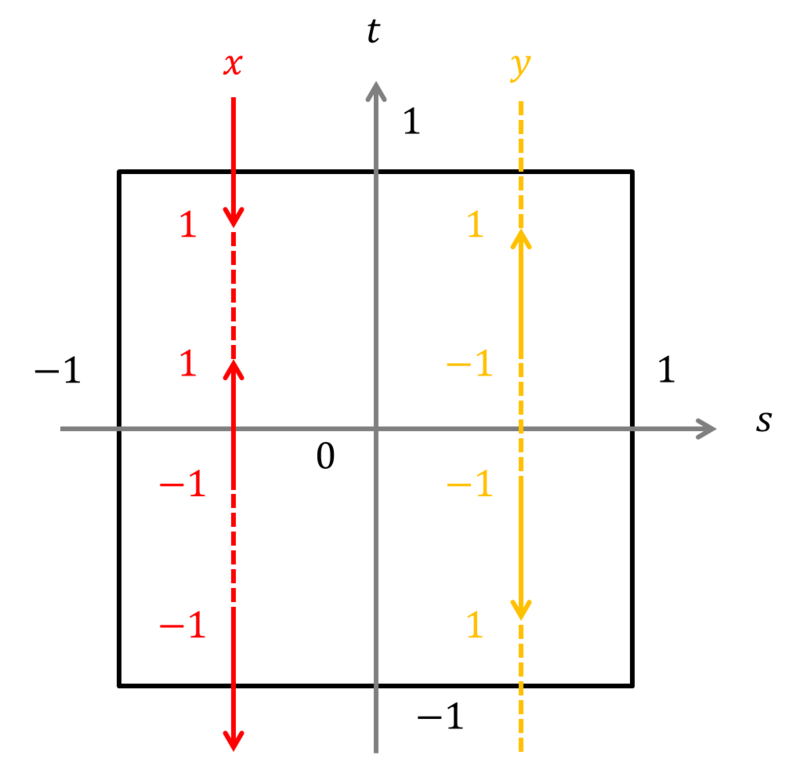
つまり，平坦トーラスを3次元+時間で捉えると，最初は一つの輪っかであり，2つに分裂してまた戻るというふうになる．平面上でのの対応を書くと，次のようになる．

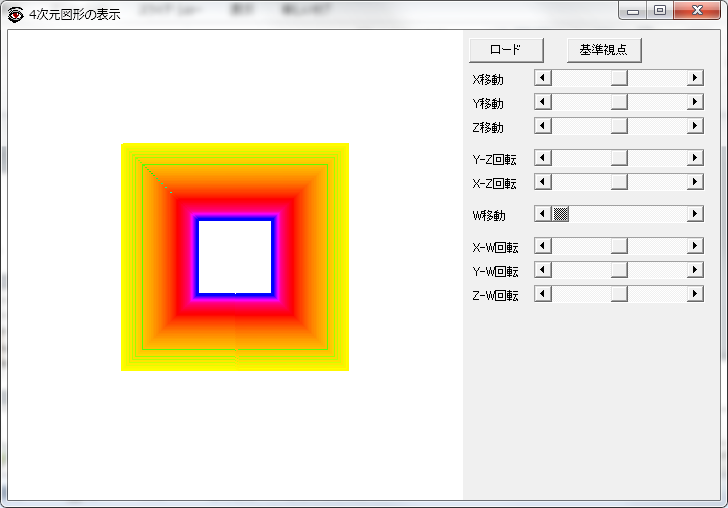
ここまで時間の断面で4次元空間を捉えたが，もっと直接的に4次元を見ることができる「4次元図形の表示」というそのままなタイトルのフリーソフトがあった．4次元空間上の座標をテキストファイルにして入力するとワイヤーで結び，3次元空間に射影したものを見ることができる．断面ではなく射影なのでこれまで見てきたものとは異なるが，平面を走査した線を4次元座標に変換したファイルを入力してみた．まあしかしこれで平坦トーラスを把握できる人はこの次元の人ではないであろう．

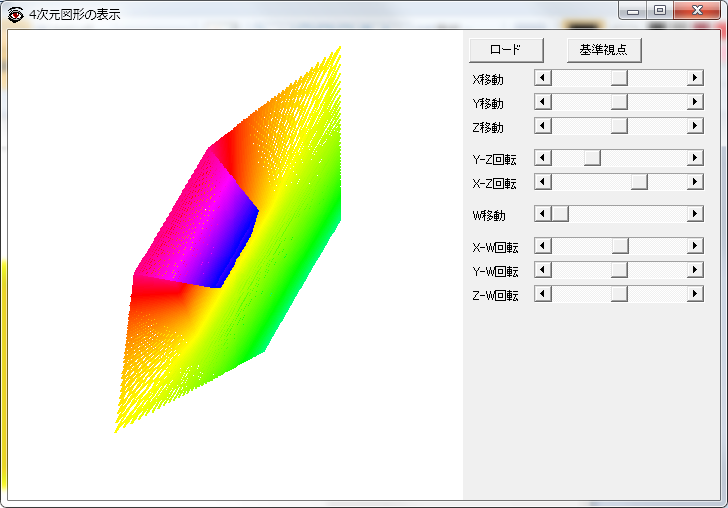
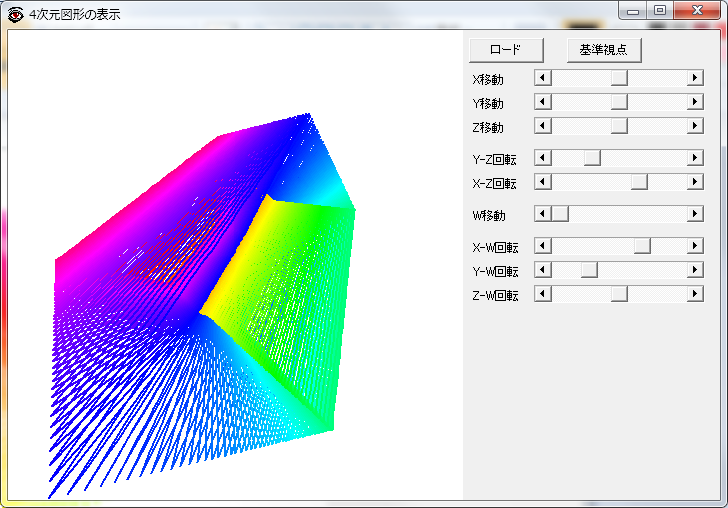
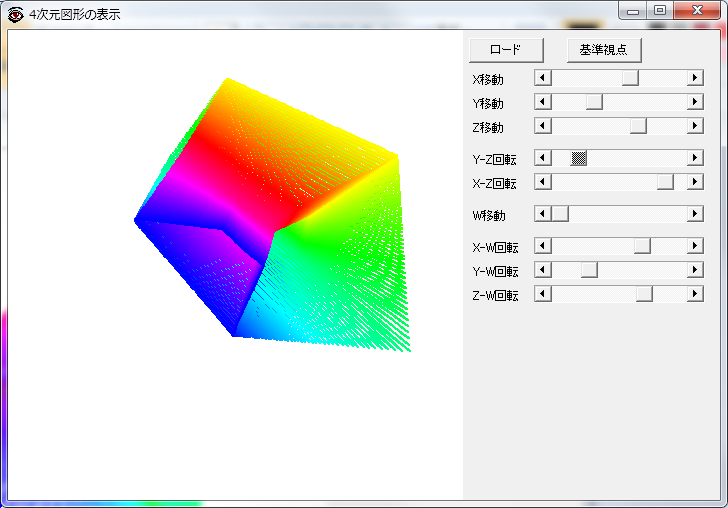
実は，最後に読み返していて気づいたが，紙で四角い筒（円筒でもよい）を作り，はこの紙の表側を，は裏側をなぞっていると考えれば紙で平坦トーラスを表現できる．つまり地図を半分に折ってから筒にすればよい．ただ，こんな記事を書いておいてなんであるが微分幾何にそれほど詳しくないので数学的にこのような向きつけ面への写像をどう取り扱うのか私はわからない．とにかく，ドラクエの世界は球でもドーナツでもなく向きつきの筒であると捉えるのが考えやすいのではないだろうか（めっちゃ図を作ったのは何だったのか）．