ドラクエの世界が見たい
「ドラクエの世界は地球のような球ではなく,ドーナツ型をしている.」という話は豆知識としてしばしば聞く話である.聞いたことがない方はこのような説明を見ると納得できるだろう.だがしかしドーナツ型というのも実はおかしな話である.地図が正確すぎるのだ.(偶然にもつい最近某掲示板でスレッドが立っていたようだ.)
我々が住んでいる地球は球体(正確には回転楕円体)であり,全世界をひずみなく平面に移すこと,つまり完璧な世界地図を作ることは不可能である.微分幾何の分野では正確な地図を書くことができる曲面のことを可展面というが,可展面であるための必要十分条件はガウス曲率が恒等的に0であることが知られている.ガウス曲率が恒等的に0な面は円柱の側面,円錐の面,そして曲線の接線で構成される面(接線曲面)の3パターンとその貼り合わせであり,半径の球面のガウス曲率は
であるため完全な地図は作れないのである.
そしてこれはドーナツも例外ではなく,そのガウス曲率は非零であるため完全な地図は作れない.よってドーナツ世界の地図上の場所によって実際の距離は変化しているはずであるが,ドラクエはそうなっていない.どこでも1マスの大きさは一定のドット数で表されている.
では,ドラクエの世界は曲面として全くありえないのかというとそうでもない.ここまであえて「トーラス」という言葉を使わず「ドーナツ」と言ってきたが,ドラクエの世界は平坦トーラスというトーラスの一種と考えることができるのである.だが,この平坦トーラスというやつは厄介なやつでなんと4次元空間の曲面である.4次元空間を考えるのはとても難しいが,なんとか平坦トーラスがどんな形か考えてみよう.
(以下,難しければ最後だけ読めばよい)
4次元空間は3次元空間+時間と考えることができる.つまり4次元空間の物体は時間的に形が変化する3次元物体ととらえることができる.よってある時刻で4次元物体を見れば3次元のものとして我々にも想像できる.これはつまりある時間で断面を作ることになるが,断面を作るとその物体の次元は1つ小さくなる.よって4次元空間の曲面である平坦トーラスをある時刻で見ると曲線になっているはずである.
このことは平坦トーラスを考えるうえで大きなヒントになる.それでは,この世界地図がどのように閉曲面をなしているのかを説明しよう.

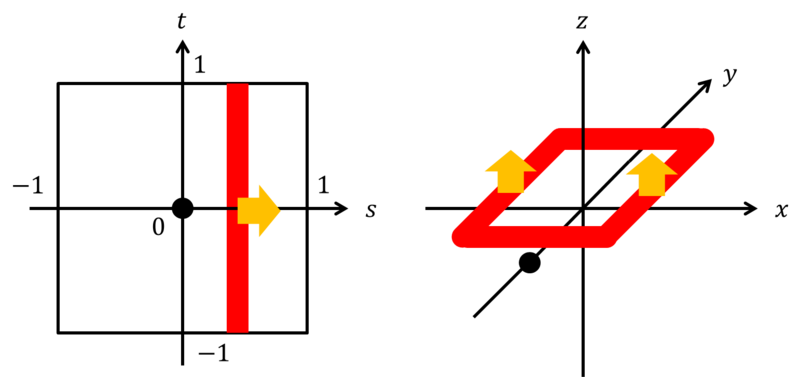
この地図上で閉曲線を書くとそれは当然4次元曲面上で閉曲線をなしているはずである.例えば下図の赤線のような線を考える.上と下はつながっているためこの線は閉曲線である.

地図上にによる座標をつけ,今考えている空間を
の3次元空間+
の時間からなるものとしよう.そしてとりあえずこの赤線に対応する閉曲線はある時刻の
平面内の閉曲線であるとし,原点は
に写っているとする.

この赤線は平面上で動いても平坦トーラス上では閉曲線を保つ.今は赤線は
上にいるが,これを
と移動させると元の位置に連続的に戻るはずである.さらに地図と平坦トーラスの場所は1対1に対応しているため赤線は4次元空間の座標として同じところを通らない.要するに輪っかが動いて元に戻ればよい.4次元空間の一筆書きのようなものである.
初期時刻をとし,とりあえず時刻とともに
の高さまで赤線を
軸正の方向に動かす.ここで時刻は
になったとしよう.

元の位置に戻さないといけないので,今度は軸負の方向に移動させる.さっき通ったところであるが,時刻が異なるので4次元空間的には違う場所である.
までおろした時点で時刻は
になったとする.

的には輪っかはもとに戻ったが,時刻が異なるので4次元空間的には違う場所である.なのでこれでゴールではない.元に戻るためには時間を戻さなくてはならない.しかし単に今までの運動を逆回しにするのでは4次元空間的に同じ場所を辿ることになるのでNGである.そこで,時間を遡りながら
軸負の方向に輪っかを動かす.
までおろしたところで時刻は
まで戻っているとする.さっき時刻
で
の高さに動かしていた赤線が見える.

このまま時間を遡りながらで
の位置まで赤線をあげる.さっきのやつと徐々に距離が縮まり,最後に合流して終了である.

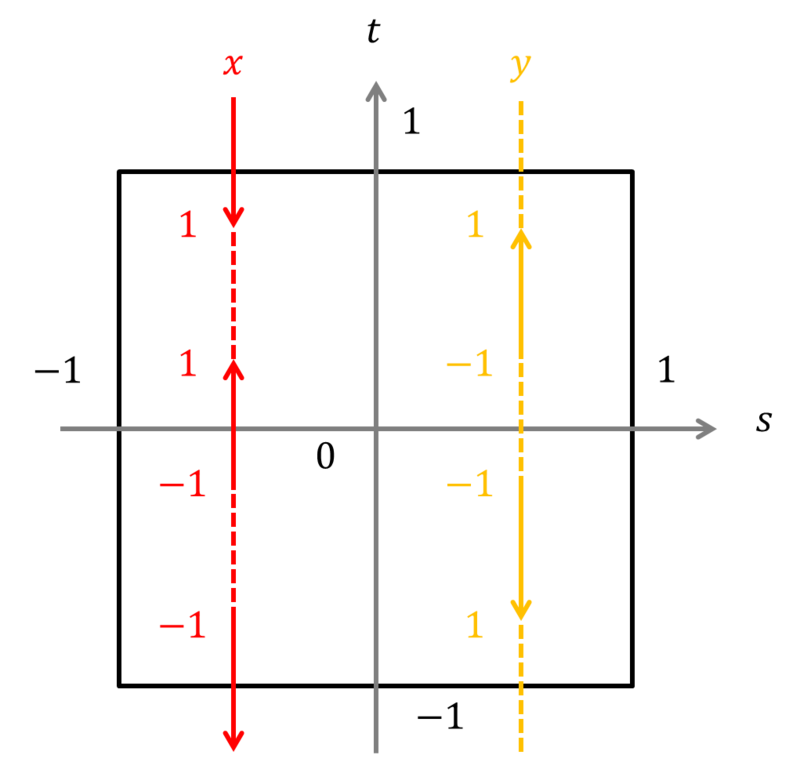
つまり,平坦トーラスを3次元+時間で捉えると,最初は一つの輪っかであり,2つに分裂してまた戻るというふうになる.平面上での
の対応を書くと,次のようになる.

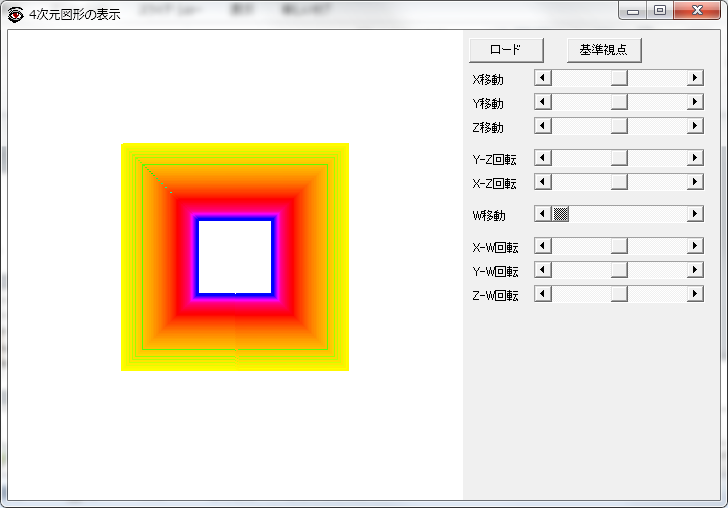
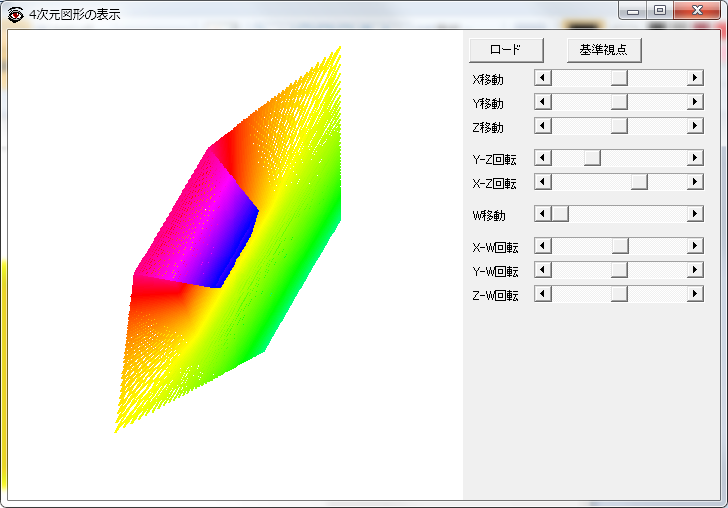
ここまで時間の断面で4次元空間を捉えたが,もっと直接的に4次元を見ることができる「4次元図形の表示」というそのままなタイトルのフリーソフトがあった.4次元空間上の座標をテキストファイルにして入力するとワイヤーで結び,3次元空間に射影したものを見ることができる.断面ではなく射影なのでこれまで見てきたものとは異なるが,平面を走査した線を4次元座標に変換したファイルを入力してみた.まあしかしこれで平坦トーラスを把握できる人はこの次元の人ではないであろう.

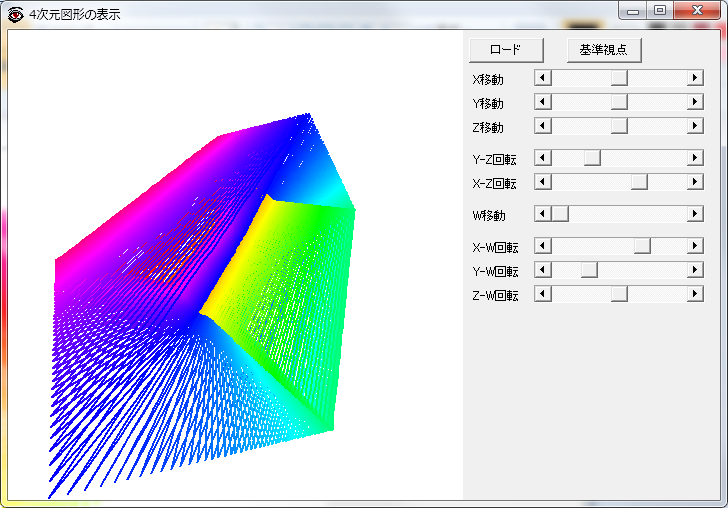
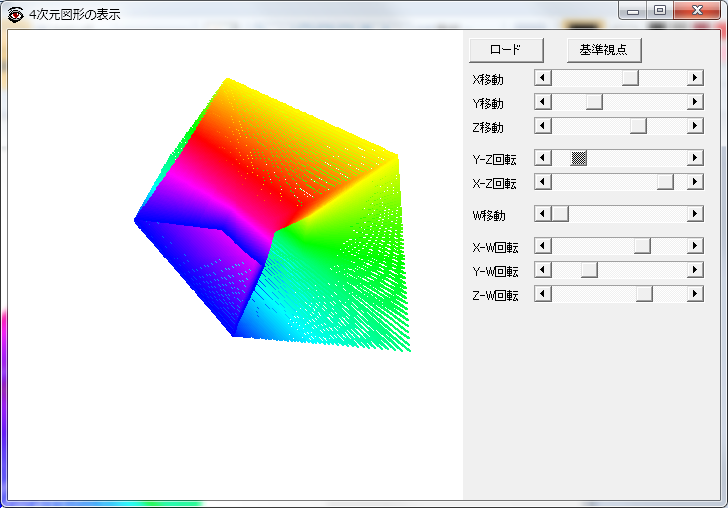
実は,最後に読み返していて気づいたが,紙で四角い筒(円筒でもよい)を作り,はこの紙の表側を,
は裏側をなぞっていると考えれば紙で平坦トーラスを表現できる.つまり地図を半分に折ってから筒にすればよい.ただ,こんな記事を書いておいてなんであるが微分幾何にそれほど詳しくないので数学的にこのような向きつけ面への写像をどう取り扱うのか私はわからない.とにかく,ドラクエの世界は球でもドーナツでもなく向きつきの筒であると捉えるのが考えやすいのではないだろうか(めっちゃ図を作ったのは何だったのか).
エタノール「シュッシュッ」キムワイプ「サッ」ミリQ「ドゥルルルルル・・・」←おまえら何なの?
彼はこれまで生物学とはほぼ無縁の生活をしてきたが,一念発起して生物系,それも実験系の研究室に所属することに決めた.彼が読んだ新書によると近年の生物学における進歩は目覚ましく,彼の妄想は現実のものとなるかもしれないと考えたのである.そして彼は先輩から実験手技を習っていた.
「まずは消毒な.霧吹きでエタノールを机に吹き付けてキムワイプで拭く.ほんで実験で使う器具もエタノールを吹き付けて乾くまで放置.」
「おお!今から実験するぞって感じですね.これで細菌が全部死ぬんすか?」
「まあそのための消毒やからな.」
「なるほど確かに.菌って空中からは来ないんですか?こうやって放置している間に埃みたいについてきたりとか.そもそもエタノールでありとあらゆる細菌が死ぬもんなんですか?こんなシュッシュしただけで.」
「う~ん…そういうふうに考えたことはなかったな.まあそんなに厳密にやらなくてもこの実験はできるで.」
「あー…そうっすか.(ほななんで消毒すんねん)」
「まあいいわ.次はこのちっさいビーカーに水をいれます.実験やるうえで水っていうたら超純水やから気いつけてな.」
「ああ.あのミリQっていう装置から出てくるウルトラピュアなH2Oのことですよね.いっつもそのノズルつきのボトルに入れて使ってるんですか?」
「そうそう.なくなったらまた入れといてな.」
「了解です.ミリQってそんなボトルに長時間入れといてもウルトラピュアなままなんですか?」
「たぶんそうなんちゃう?そこまで考えたことなかったけど.」
「ウィッス(この人に聞いても全然わからん…)」
実際にこんな話があったわけではないし,この会話の発言は全て正しいとは限らない.だが,多くの実験系の研究室の学生は,教わった細かな手順が厳密にどのような効果を持つのか把握していないのではないだろうか?実際にはこの会話の先輩のように疑問にも思わなかった人が大半で,その他は彼のように心に疑問を抱えながら実験をしているのであろう.私もそういうその他少数の一人であるが,研究成果への圧力に抗ってこれらの疑問を解決すべく模索している.
そういう訳で,図解入門 よくわかる最新抗菌と殺菌の基本と仕組みという本を読んでいた.実験室における殺菌,消毒というよりは一般的な殺菌のしくみであるとか抗菌製品の原理についての本であったが,なかなかためになった.
まず今まで知らなかったのが種々の○菌という言葉の定義である.対象の微生物を全部殺す,あるいは除去することは滅菌といい,殺菌と言うと殺すにしても全てとは限らなくなる.また消毒という言葉は病原性微生物の殺菌である.つまりコンタミを気にするような実験では病原性微生物に限らず邪魔な菌を殺すことが必要であろうから,その場合は消毒と言うよりは殺菌と言う言葉の方が適しているだろう.ついでに言うと,この分野では殺滅という言葉も使われるようである.過酢酸の効果に「35%濃度では,すべての微生物を30秒で殺滅」と書かれておりなんとなく過酢酸にかっこよさを感じてしまった.
実験室との関連を感じたのは「除菌」の基準についての部分である.一時期抗菌だの除菌だのを謳い文句にした粗悪な品質の製品が溢れたのを境に,最近では基準となる試験を通過した製品が「除菌」書けるようになっているらしい.例えば除菌ウェットワイパーと言うためには,150gの重さで5往復拭いて残った菌が,除菌効果のない布で試験した場合よりも2桁以上減っていなくてはならない.ドラッグストアでよく見かける除菌ウェットワイパーはたいていアルコールが使われている(と思う)が,ここから類推するにエタノールとキムワイプで机を拭くのもこれくらいの効果があるのではないかと考えられる.また,CELAという次亜塩素酸水の商品ページでは,除菌試験効果としてCELAで湿らせたキムワイプで拭いた机と拭いていない机に寒天を押し当てて培養し,CELAではコロニー形成が見られないという結果が示されている.ただ,他の実験結果では並列してアルコールによる結果とも比較しているのに対してこの実験結果はCELAと無処理群との比較になっている.実はアルコールでもなかなか効果があるのではないだろうか?
さらに殺菌,除菌について知りたい方は何かしら本を参考にしていただくとして,超純水についても少し書いておこう.超純水に関しては超純水超入門という日本ミリポア社が編集した本が出版されており,さすがというべきかかなり詳しい.
この本によるとやはり超純水は使用直前に採水するのが原則であることがはっきりと示されている.水の純粋さは比抵抗によって表され,超純水では18.2MΩ・cmに達する.しかし採水直後から二酸化炭素などが溶け込むため,比抵抗は急激に減少し,10分後には10MΩ・cmに,60分後には4MΩ・cmに減少する.Wikipediaによると比抵抗1~10MΩ・cmの水は純水と呼ばれるので,使用時間によっては超純水というより純水であると認識した方がよいだろう.他にも,超純水に指をつけてしまった場合にどんなイオンがどれくらい混ざってしまうかであるとか,ガラス電極では実は超純水のpHを図ることができないこと(ガラス電極でpHを測定するには十分な導電率が必要)などがデータで示されている.
実験手技の伝達ではしばしば定性的な説明がなされがちであるが,このようなしっかりしたデータがあると大いに参考になる.まあ,そんなに気になるなら自分でやれよという話であるが.
片側だけでは都合が悪い
関数を扱う上で連続性があるのとないのとでは扱いやすさがだいぶ異なる.関数は制限がなければいくらでも変なものが考えられるが,連続性という条件が付いているだけでヤバい関数を大幅に締め出すことができてうれしいのである.とはいえ,連続だがいたる所微分不可能な関数というのもあり,連続性がついていてもまだ変な関数はいくらでも考えられる.
連続関数には局所可積分という性質がある.1変数関数が局所可積分であるとは,
の定義域に含まれる任意の閉区間
において積分
が値を持つことをいう.閉区間のどこかで連続関数は最大値,最小値をとるので積分が有限の値になるのは容易に想像できるだろう.
だが少し縛りを弱くして片側連続だけにすると局所可積分性は失われる.例えば
は左連続であるが周りで積分すると発散してしまう.局所可積分が欲しければ片側連続とは別で要求するか両側連続にしなくてはならない.
対数表に「素数」の表がついている?
この記事は 明日話したくなる数学豆知識アドベントカレンダー の 27日目(!?)の記事です。(26日目:対数表には「素数」の表がついている )
いやー.数学アドベントカレンダー終わりましたねー.中々大変でしたよあれだけ記事を書くのは.
ところがねー.なんか終わってないっぽいんですよねー.tsujimotter氏のブログを見ると.「明日は 遠藤逸ノ城さん あたりが書いてくれる・・・といいな。なんてね。笑」とか書いてあるし.まあ,軽い気持ちで書きますか.
昨日のtsujimotter氏の記事によると,かの有名なガウスは15才の誕生日に対数表をプレゼントされ,巻末の素数表を見つけたとのことです.そしてtsujimotter氏が試しに日本の対数表を開いてみたところ,やはり巻末に素因数分解の表が載っていたというお話でした.
実は私も対数表を持っています.しかも偶然にも私も14か15の時に対数表を買ってもらいました.対数を使えばを具体的に計算しなくても何桁かわかるとかいう話を本で読んだころで,ジュンク堂で見かけた対数表が欲しくなったのです.

久しぶりに開いてみましょう.ほぼ数字しかない本ですが,ちゃんと目次があります.

実はいきなり数値表になっているのではなく,対数計算に関するいくつかのTipsが書かれています.続きの目次を見てみましょう.

この本には三角関数の値も載っているのでその解説が続き,それからいよいよ常用対数表,三角関数表がきてこの本は終わりです.
はい.そうです.この本には素数表はついていません.最後のページを見ても三角関数表で終わっています.

まあ,たしかに素数表がついていると便利なんですけどね.中にはついてない対数表もあるという話でした.私が買ってもらった対数表に素数表がついていたら,私の名前が関数につけられるほどの活躍ができたかもしれませんね.ムフフ
すごい判別式
この記事は 明日話したくなる数学豆知識アドベントカレンダー の 22日目の記事です。(21日目:アルキメデスと円周率 )
このブログを始めるきっかけとなった明日話したくなる数学豆知識アドベントカレンダー としてはこの記事は最後である.およそ2日に1回のペースで更新するあたり「どんな暇人か」と思われているのかもしれないが,記事執筆に追われたおかげで暇人ではなくなった.今まで人にあまり言わずに持っていた数学ネタを一気に放出したので,「もうネタがありません!」という状態なのであるが,ブログ自体は残しておいて数学に限らず何かネタを思いついたら気ままに書いていくこととしよう.なお,数学豆知識自体はあと3日間あるので,明日以降の記事も皆様楽しみにしていただきたい.
さて,今日の話は判別式についてである.判別式というとを思い浮かべるであろう.専ら2次方程式でしか判別式を使ったことがない人がほとんどであろうが,少し詳しい人は3次方程式や4次方程式の判別式を知っているかもしれない.そんな判別式は方程式の実数解の個数を求めるためのものと捉えられている節があるが,実際には重解があるかどうかを見るためのものである.というのも
次方程式の判別式
は,解
によって
と定義されるのである.方程式に重解があれば当然判別式は0になり,逆に判別式が0であればその方程式には重解がある.ただしから重解が何重であるかを知ることはできない.2次方程式の判別式の正負および零判定で解の個数がわかるのは,解の個数のパターンが0個,1個,2個の3パターンしかないからである.高次の方程式において解の個数を判定するには,判別式の他にさらに別の式を用意するというような工夫が必要となる(3次の例).
なお,上の判別式の定義は方程式の係数ではなく方程式の解で書かれている.しかし判別式が方程式の係数で書けることは保証される.というのもこの判別式は差積の2乗になっているため解の対称式となるのである(tsujimotter氏のガロア理論の話).5次以上の方程式が解けないことは知られているが,判別式を書くことはどんな次数でもできるのである.
ただし,正確には「判別式を書くことは原理的にはどんな次数でもできる」ということである.では実際に100000次方程式の判別式は書けるだろうか?ここで,京都大学の木村欣司氏の17次方程式の判別式の計算報告を見てみよう.
次方程式
の判別式の項数は,21976689397
ディスク容量では,427,470,114,659byte
項数はおよそ220億個あり,手計算でやろうなどと言うと「判別式計算にその生涯を費やした人物」として語り継がれることは必至である.計算機上でもその計算結果は427GBの容量を食う.ちなみにこの計算は10時間で終わったそうであるが,32コアCPU,1TB超のメモリを持つマシンでの話である.もちろんこの計算も工夫に工夫を凝らした手法で行われたものであり,17次方程式の判別式の計算と言うのは記録的なもののようである.ましてや100000次方程式の判別式など実際にはできそうにもない.
数学の命題を素直に捉えると,このように思いのほか裏切られることがしばしばある.そのため数学者はしばしば嘘つきに見えてしまう.「~はできる」とか言っておいていざやろうとすると「無限に分割することが必要だ」とか,「ここで有理数と無理数の点で分ける」だとか言いだし,挙句の果てにはいつまでたっても終わらない手順を続けようとする.彼らが見ている真実は果たして現実なのだろうか?
たのしい積分
この記事は 明日話したくなる数学豆知識アドベントカレンダー の 20日目の記事です。(19日目:期待値とある値以上の確率との関係 )
高校三年生だった年の今頃は受験勉強に明け暮れていた.山ほど数学の問題を解いて勉強した結果,大学の線形代数,解析学の最初の方は高校で得た知識でなんとかできたが,内容が発展していくとだんだん高校の生半可な知識では歯が立たなくなっていった.結局大学数学は高校の知識を捨てて最初から学びなおすこととなり,あれだけ勉強したのは何だったのかと呆然とすることとなった.それでもあの受験勉強の経験で今でも役に立っているものがある.それが正確に,速く計算する技術である.
中でも今でもよく使うのは部分積分による不定積分の暗算である.部分積分の公式は
であるが,こうして式で書くと普段私が使っているようなイメージとは違うような印象を受ける.私の計算も確かにこの通りなのであるが,この公式からは被積分関数を「作っている」感じがしないのである.例えば,の積分では私は次のように考える:
(1)より,
と掛ければ
ができるなと考えておもむろに
と書く.
(2)を微分した結果を下に書く.目的の
が現れるが,余分なものも出てくる.
(3)目的の項だけが残るように,打ち消す項を下の行に追加する.
(4)より,
と掛けて係数を調整すれば
ができるなと考えておもむろに
を上の行に追加する.
(5)を微分すると,
の他に
が現れるので,それを下の行に追加する.
(6)余分な項を打ち消すため,下の行にを追加する.
(7)なので,上の行に
を追加する.
(8)もう余分な項は出てこないので,これで完成.上の行が不定積分になっているので,積分定数を追加して答案に書く.
(9)この例ではうまくいったが,時には下の行に積分できない関数が現れたり,永遠に積分が終わらなくなることがある.具体的には,(1)でが現れる不定積分として
から出発したが,
から出発してしまうと
の次数が上がっていくだけで一向に終わらない.こういう場合には出発する関数を変えてやってみるとうまくいくことがある.
私は部分積分が面倒で嫌いだったのであるが,この計算手法なら無駄にインテグラルを書かなくてもよい.慣れてくると下の行を書かなくてもだいたいできるようになってくるので,暗算で積分ができるようになる.模試で隣の席の生徒がえっさほいさと途中式を書いている中,一行でスパッと積分が書けると気持ちいい.「たのしい算数」は全く楽しくなかったが,当時の私にとって積分はとても楽しいものであった.
おつりでフラクタル
この記事は 明日話したくなる数学豆知識アドベントカレンダー の 18日目の記事です。(17日目:正十七角形は作れる )
たしか2年くらい前にこんなコピペが流行った(おそらく初出はこれ?):
コンビニで代金が777円だったとき。
777円の表示を見たバイトの兄ちゃんが「おーっ」とか言ってるので、
すかさず1332円出した。
キョトンとしてるので、「まあいいからレジ売ってみな」言ってやった。
レジには釣り555円の表示。
バイトの兄ちゃん絶叫してた。
さすがにここまできれいなおつりのもらい方をしたことはないが,財布の小銭が少なくなるような支払いはほとんどの人が日常的に行っているのではないだろうか.このようなおつりの計算方法は欧米では困惑されるという話をよく聞くが,この違いは等価交換の考え方の違いによるらしい(日本と西洋のお釣りの計算方法と等価交換).
それはさておき,今から2年前の2012年,現在中央大学理工学部の山本健氏の"Fractal behind coin-reducing payment"という論文が Chaos, Solitons & Fractals という学術雑誌に掲載された.日本語にすると「硬貨を減少させる支払い方でのフラクタル」となる.実はお金の支払い方にフラクタルが潜んでいるのである.
小銭支払の達人が,1000円未満の買い物を延々と繰り返すことを考える.ただし,所持金が足りない時は1000円札がどこからともなく現れるとする.小銭支払の達人なので,おつりの数字を時系列に見ていくと,500円,あるいは100円といったきりのいい数字が多くなる.そこで,回目の買い物でのおつりを横軸に,
回目の買い物でのおつりを縦軸にして赤いしるしを打っていくと,なんと次のようになる(図は論文より):

図の右上には典型的なフラクタル図形であるシェルピンスキーのギャスケットが示されているが,そっくりである.
ではなぜこのようなフラクタル図形になるかを説明しよう.まず,最適支払手法は次の2ステップで表される:
(1) 会計後の所持金を最小枚数の小銭で表す.
(2) 最小枚数で表した会計後の小銭を現在の小銭と比較し,減る硬貨が会計で使用する硬貨に,増える硬貨はおつりに対応する.
一つ例を挙げよう.今682円持っているとし,117円の買い物をしたとする.会計後の所持金は682-117=565円である.565円を500円玉,100円玉,50円玉,10円玉,5円玉,1円玉の枚数で表すと,
( 1, 0, 1, 1, 1, 0)
となる.一方,現在の所持金682円は枚数で表すと
( 1, 1, 1, 3, 0, 2)
である.比較すると
( 0,-1, 0,-2,+1,-2)
である.よって122円支払って5円玉1枚を受け取るのが最適支払となる.
おつりの時系列をもう少し詳しく見るため,10円玉の枚数に着目しよう.回目の会計前の10円玉の枚数を
とし,
回目の会計でもらうおつりを
とする.上のアルゴリズムより,
である.を考えると,
となる.最適支払を続けている限り,10円玉の枚数は4枚を超えない.つまり各で
である.これと上の式を考えると
となる.この条件を図で示すと,連続するおつりの組み合わせは図の赤色のマスでなくてはならないことになる:

今の話は10円玉を1円玉,100円玉に置き換えても全く同じである.5円玉,50円玉,500円玉の場合には,それぞれの最大枚数は1枚,つまりであるので,
となる.図で示すと次のようになる:

これでフラクタル図形の準備はできた.連続するおつりのプロットでは,横軸も縦軸も0円から999円までである.これを500円玉の枚数で見ると,0円から499円までが0枚,500円から999円までが1枚となる.これに今示した条件を重ねると次のようになる:

次に,100円玉の枚数で見ると,金額100円ごとに1枚増え,0枚,1枚,2枚,3枚,4枚,0枚,1枚,2枚,3枚,4枚となっている.全体を4分割すると上で見たマスの塗り方が適用できる.この条件は全ての硬貨で成り立っていないといけないのですでに500円玉の条件で除外された領域は外す.ごちゃごちゃ言うよりも結果を見る方が早い:

すでにその形が見えてきた.今度は50円玉の条件を適用してみる:

これにさらに10円玉,5円玉,1円玉のルールを適用すると論文の図になる.キーポイントは硬貨を価格順に並べたとき,整数倍になっていることである.このおかげで一つ下の硬貨のルールを適用する際にきれいな分割ができることになる.逆に言うと,この硬貨の倍数性が成り立っていない貨幣体系ではフラクタルにならない.例えばドルの場合の硬貨は50セント,25セント,10セント,5セント,1セントであるが,25セントは10セントの整数倍ではない.連続おつりプロットを書くと,微妙に崩れた形になってしまう(図は論文より):

一時日本で2000円札と言うものがあったが,これがあると札の系列が10000円,5000円,2000円,1000円となって倍数性が崩れてしまう.やはり廃れて正解だったようだ.